Purpose: To explain the orientation angles used for Inertial Labs devices and how they relate to one another.

Last Updated: August 2019

What's the difference and why does it matter?

Euler angles are generally what most people consider when they picture 3D space. Each value represents the rotation in degrees (it could technically be in any units) around one of the 3 axes in 3D space. Most of the time you will want to create angles using Euler angles because they are conceptually the easier to understand. The flaw is that Euler angles have a problem known as the gimbal lock that prevents certain rotations when two axes align. The solution: quaternions.

How to convert between Quaternion and Euler angles?

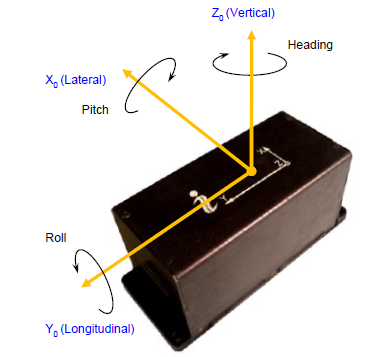
Fig. 1.

Define coordinate system 'x_oy_oz_o' to be fixed to the carrier object where 'x_o' axis is lateral and directed to the right, 'y_o’ axis is longitudinal and directed forward, 'z_o' axis is normal and directed vertical. At usual installation of the unit on carrier object the units appropriate axes should be parallel to the axes as above Fig. 1. shows. Also, it is possible to install the unit in any known position relative to the object with known alignment angles (see APPENDIX B of the units Interface Control Document (ICD) for details).

The Inertial Labs^TM unit calculates orientation of the coordinate system ‘x_oy_oz_o’ fixed to the carrier object with respect to Cartesian geographical reference frame ‘xyz’ where axes ‘x' and ‘y’ are in the level and directed to the East and North, and 'z’ axis is directed up. Such reference frame is also known as ENU (East-North-Up) Earth-level frame.

Measured angles are the standard Euler angles of rotation from the Earth-level frame to the object frame: heading K is first, then pitch q, and then roll g -- see Fig. 2.

Notes:

1. Positive direction of heading is clock-wise. So heading K is shown with minus sign on Fig. 2.

2. In different applications “heading” is also known as “azimuth” or “yaw”; “pitch” is also known as “elevation” or “tilt”; “roll” is also known as “bank”.

Due to the definition of Euler angles there is a mathematical singularity when the object longitudinal y₀-axis is pointed up or down (i.e. pitch approaches ±90°). This singularity is not present in the quaternion or directional cosine matrix (rotation matrix) presentation.

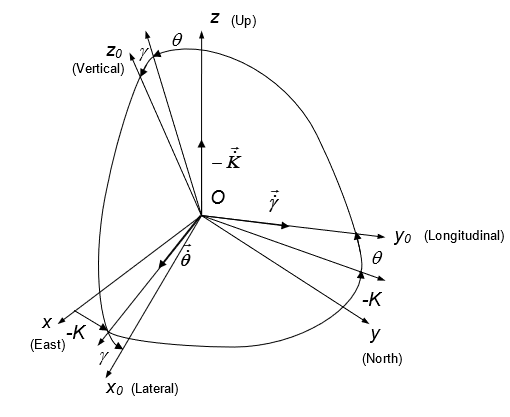Fig. 2. Transformation of coordinate systems

Directional cosine matrix (DCM) is the rotation matrix C from the object body reference frame ‘x_oy_oz_o' to the geographical reference frame 'xyz’. According to Fig. 1, DCM can be represented through Euler angles as:

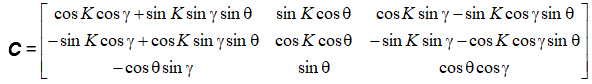Equation 1

Or, Euler angles can be calculated from elements c_ij of directional cosine matrix C:

Equation 2

Also the Inertial Labs^TM unit provides orientation output in quaternion Q form which is a hyper-complex number with four components

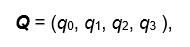Equation 3

where q₀ is real part, q₁, q₂, q₃ are vector part. In other words, q₀ represents the magnitude of the rotation, and the other three components represent the axis about which that rotation takes place.

With only four components, quaternion representation of orientation is computationally efficient. However, manipulation of quaternions is not intuitive, so their use in place of directional cosine matrices may increase the chances of mistakes being made.

Quaternion Q is converted to directional cosine matrix C using the next expressions:

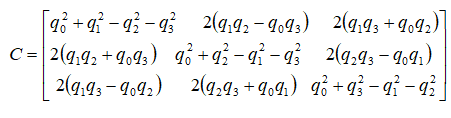Equation 4

The reverse conversion from directional cosine matrix C to quaternion Q is following:

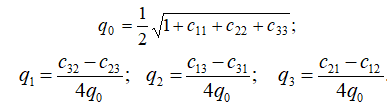Equation 5

The expressions above in Equation 5 are widely used but they have singularity at q₀ = 0. Therefore the Inertial Labs^TM unit uses other expressions that have no singularity:

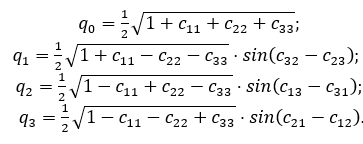Equation 6

At necessity to calculate Euler angles from quaternion, calculate elements c₁₂, c₂₂, c₃₁, c₃₂, c₃₃, according to Equation 6, and then use Equation 2:

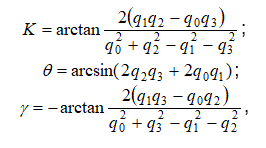Equation 7

where arctan is four-quadrant inverse tangent.